あるごりずむ体操

初めに

今回は当り判定と三角関数について載せます。

当り判定

四角形同士の当り判定

四角形同士の当り判定はたぶん一番使われる当り判定だと思います(2Dでは)。軽いし使いやすいし。マスターしましょう。

中心間の距離を利用する方法

この方法では、四角形があたったときの中心間の距離に注目します。二つの四角形が

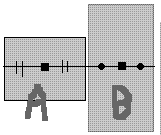
こんな状態になった時、Aの中心とBの中心間の距離はAの横幅の半分+Bの横幅の半分以下になっています。これを利用すれば当り判定ができます。

実際にソースみたほうがわかりやすいかもしれません。

function HitCheck(x1,y1,Width1,Height1,x2,y2,Width2,Height2:Integer):Boolean;
//Widthは横幅の意、Heightは縦幅の意。
begin        ///andを使用しないのは軽量化の為。
  if (Abs((x1 + Width1 / 2) - (x2 + Width2 / 2)  ) <=  (Width1 + Width2) / 2) then
    if (Abs((y1 + Height1 / 2) - (y2 + height2 / 2)  ) <=  (Height1 + Height2) / 2) then
      Result:=True else Result:=False;
end;

この方法は結構軽いです。

TRectを使う

この方法は凄く便利でなおかつ簡単なのですが、Delphi限定の技です。(他の言語でも似たようなことはできますが)

Dephiには四角形を表す構造体TRectがすでに用意されており、さらにTRect同士の当り判定を行う関数も用意されています。

そんな便利なものをつかわない手はありません。使ってみましょう。

用意

function HitCheck(RectA,RectB:TRect):boolean;
var  tmprect:TRect;
begin
  //重なっていればtrueが返ります
  Result:=IntersectRect(tmprect,RectA,RectB);
end;

実装

procedure TFrom1.Main;
begin
///”四隅の点を渡したほうが簡単では？”と思われるかもしれません。でも、TRect型を渡したほうが後々便利になってきます。
  if HitCheck(
       Rect(x1,
            y1,
            x1 + Width, //横幅
            y1 + Height,  //縦幅
         )
       Rect(x2,
            y2,
            x2 + Width2,
            y2 + Height2
         )
     )
end;

Rectというのは四隅の点を引数として受け取ったときTRect型に変換する関数です。あらかじめTRect型のものを用意してあればそれを渡せば良いのでRectを使う必要はありません。

格闘ゲームを作る際は予めTRect型のものを用意しておいたほうが当り判定の調節がし易くなるため便利です。少しソースコードが長くなってしまいますが。

円と円の当り判定

今回も二つの円の中心間の距離を考えます。

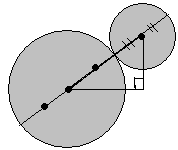
この状態のとき、中心間の距離は二つの円の半径の合計以下になっています。

つまり、中心間の距離を三平方の定理で求めれば当り判定ができます。どのようにやるかみてみましょう。

function CircleHitCheck(x1,y1,r1,x2,y2,r2:integer):boolean;
begin
  if sqrt( (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)) <= (r1 + r2) then
    Result:=True else Result:=False;
end;

さて、この方法では平方根を使用してます。しかし、平方根を求めるという事は非常に重くなる作業です。そこで、両辺を二乗して高速化します。

function CircleHitCheck(x1,y1,r1,x2,y2,r2:integer):boolean;
begin
  if (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= (r1 + r2) * (r1 + r2) then
    Result:=True else Result:=False;
end;

三角関数について

はじめに

三角関数とは直角三角形のある角に対する各辺の比を求めるもので、三角関数を利用すればいろいろなことができます。

具体的には弾を一定の方向に打ち出したり、ホーミング弾を作ったり、くるくるくるりんのような円移動をしたり、波移動をしたり。QDでは三角関数を利用すれば画像の回転ができます。

とても便利なものなので、是非使いこなせるようになってください。

sin,cosを利用する

sinはサインのことで正弦関数、cosはコサインのことで余弦関数を意味します。

function Sin(X: Extended): Extended;

Sin関数は引数のサインを返します。

Xは実数型の式です。Sin は，ラジアン単位で指定した角 X のサインを返します。

Delphiヘルプより

三角関数のさらに詳しい説明をここでするのは難しいので、三角関数についてもっと知りたい人は教科書でもよんどいてください。ここではsinとcosの実践的な使い方の説明をします。

ちなみに、ここで書くソースコードはOnTimerイベント内にかかれていることにし、x,y座標には画像が表示されるものとします。また、aはExtended型の変数とします。

波のような動きをさせる

a:=a + 0.5;
y:=300 + Integer(Trunc(sin(a) * 100)); //100は波の幅、300は波の軸。
x:=x + 5;             //Trunc関数は戻り値がInt64なので注意。

このようにすると、画像が波のような動きで右に移動します。

円移動をさせる

a:=a + 0.3;
y:=300 + Integer(Trunc(sin(a) * 100)); //100は円の半径、300は円の中心。
x:=300 + Integer(Trunc(cos(a) * 100));

このようにすると、画像が円移動します。

ななめ移動をさせる

y:=y + Integer(Trunc(sin(1) * 5)); //1は動かす角度。ラジアンなので注意。
x:=x + Integer(Trunc(cos(1) * 5)); //5は速度。

このようにすると、画像がななめに移動します。いろいろ応用できますね。

三角関数をつかえばほかにベクトルの当り判定や三角形の当り判定などさまざまなことができて便利なのですが、とりあえず載せるのはここまでにします。

ArcTan2を利用する

ArcTan2関数を使えば二点間の角度を求めることができます。

function ArcTan2(const Y, X: Extended): Extended;

ArcTan2関数は、ArcTan(Y/X)を計算して、正しい象限の角度を返します。XとYの値の範囲は-2^64〜2^64で、Xは0になりません。戻り値は、-Pi〜Piラジアンになります。

Delphiヘルプより

普通に使うだけでは1つの点の角度しか求められませんが、工夫すれば二点間の角度をもとめることもできます。例。

Result:=ArcTan2(y1 - y2,x1 - x2);

渡すのはyが先というのに注意してください。こうすれば(x1,y1)と(x2,y2)間のラジアン角度がResultに代入されます。

先ほど説明したsin,cosを組みあわせればホーミング弾が打てますね。